送電建設技術者のためのニューラルネットワーク超超入門(4/4)
4.重みパラメータ
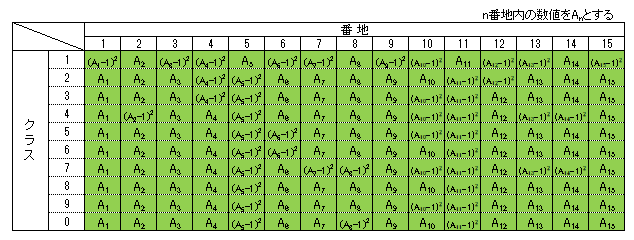
上図の緑色の部分が今回のニューラルネットワークの「重みパラメータ」である。
この「重みパラメータ」に従って、例えば1番地が1(A1=1)の場合、「クラス1」に対して(A1 - 1)^2 = 0が加算される。
(詳しくは数字認識EXCELをご参照)
このニューラルネットワークでは、入力層の15個のニューロンが重みパラメータを介して出力層の10個のニューロンに影響すると考えて頂きたい。
今回EXCELで作成したのは重みを持つのが1層だけの最も単純なネットワークであるが、
この層をどんどん重ねて深くしたディープなニューラルネットワークをディープラーニングと呼ぶようだ。
今回の例は
・数字を描くセル(入力層)は5行3列の合計15と少ない
・【0】~【9】までの数字の表現パターンは各々1つ
・セル内(各番地)の数値は「0」か「1」
・各クラスへの加算は0か1
と非常に単純であったため、最適な重みパラメータを手作業にて作成出来た。
しかし、例えば入力層が20行20列の400個になり、数字の表現パターンも手書きで個人差が有るような場合は重みパラメーターの組み合わせは無数にあり、
最早手作業や試行錯誤にて作成するのは不可能である。
ニューラルネットワークにおいて最も重要な事は大量のデータを基に「最適な重みパラメータの値を自動で獲得すること」であり、
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
でもこの手法について多くの紙面が割かれている。(そしてこの手法が大変面白い!!)
問題解決の手段にニューラルネットワークを使う場合
・問題を解決するために最適な層の深さ
・層と層を繋ぐ重みパラメータ
について適切に設定することが必要である。
ニューラルネットワークのさわりのご紹介はここまでだが、正直言って今の私の理解の範囲では「これが人工知能と言えるような代物か?」との感想だ。
しかし、この世界はまだまだ奥が深そうなので、もう少し探索して更に理解を深めてみようと思う。
そうすればまた違った感想になるのではないかと期待している。


