鉄塔設計, 鉄塔基礎設計, 有限要素法解析, 構造物強度計算, 耐震設計 株式会社スタークス

2. 平面トラスの部材剛性マトリクス

有限要素法の教科書ではこの後、フックの法則やエネルギー保存則といった話になるのだが、私達が実務をする上で知りたいのは、具体的な問題をどう解くのかである。

結論を言うと、任意のi-j部材(トラス材)の材端力(外力)と材端変位の関係の一般式は以下の様になる。 (実務上は「こういう物だ」との理解で何ら問題ない)

ここで、c=cosθ、s=sinθ
X,Yは各節点の材端力、u,vは各節点の変位
Eは部材の弾性係数、Aは部材の断面積、lは部材の長さである。

上式は以下の様に表すことが出来る。

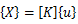
それぞれ、
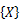 を材端力ベクトル
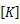 を剛性マトリクス
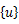 を材端変位ベクトル
と呼ぶ。

剛性マトリクスと呼ばれるのは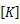の部分であるが、 全体の見通しを良くするために、材端力ベクトルと材端変位ベクトルも含めた式で以下説明する。

今回題材とする鉄塔頂部の節点番号を以下の様に定義し、節点1からXの正方向に1.00の外力(材端力)を作用させる。
部材は部材1-2と部材1-3の2本なので、上に示した部材の剛性マトリクスも全部で2つ出来ることになる。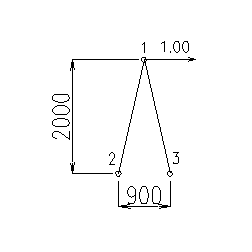

このモデルでは「部材1-2」と「部材1-3」の長さ、断面積は同じなので、計算も簡単である。