鉄塔設計, 鉄塔基礎設計, 有限要素法解析, 構造物強度計算, 耐震設計 株式会社スタークス

3. 軸力、せん断力、曲げを受ける部材の剛性マトリクス

軸力、せん断力、曲げを受ける部材の部材座標系における材端力と材端変位の関係(剛性方程式)を示す。

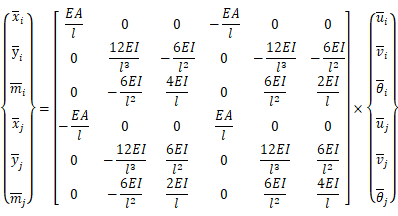
上式は以下の様に表すことが出来る

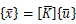
それぞれ
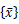 は部材座標系での材端力ベクトル
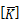 は部材座標系での剛性マトリクス
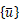 は部材座標系での材端変位ベクトル
を示す。

xは軸力、yはせん断力、mはモーメント
uは軸方向の変位、vは軸と垂直方向の変位、θは回転方向の変位である。

部材が任意の方向を向いている場合の座標変換マトリクスは以下になる。

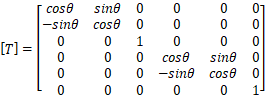
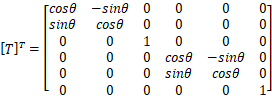
ここで、
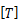 ：全体座標系から部材座標系への変換マトリクス
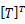 ：部材座標系から全体座標系への変換マトリクス

全体座標における剛性マトリクスは

で表すことが出来る。

これより全体座標系における剛性方程式は以下になる

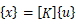
それぞれ
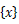 は(全体座標系での)材端力ベクトル
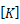 は(全体座標系での)剛性マトリクス
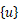 は(全体座標系での)材端変位ベクトル
を示す。

ここまでが一般論であり、こういった一般論を詳しく(小難しく)述べている書籍は山ほど有る。
しかしながら、我々技術者が最も求めている「具体的な問題の解き方」について分かり易く解説している書籍は私が知る限り存在しない。
存在しないのであれば自分で作ってやろうというのが今回の試みである。