鉄塔設計, 鉄塔基礎設計, 有限要素法解析, 構造物強度計算, 耐震設計 株式会社スタークス

7. 全体剛性マトリクスの作成

今回のテーマで扱うのはラーメン構造であり、1つの節点に3つの自由度(軸変形、せん断変形、曲げ変形)が存在する。
よって全体剛性マトリクスは「節点数×3」次の正方行列となる。

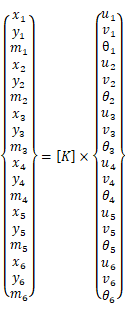
今回題材としている構造モデル全体の剛性方程式は以下の式になり、は6×3=18次の正方行列である。

それでは、5つの部材剛性マトリクスから構造物全体の全体剛性マトリクスを作成してみよう。

全体剛性マトリクスを作成する前に各部材剛性マトリクスの拡張を行う。
部材1-2を例にすると

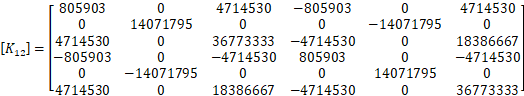
これより、部材1-2に関する剛性方程式は以下になる。

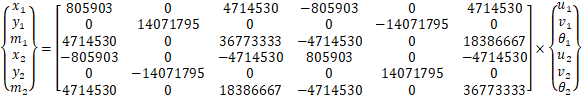
これを、6つの節点を持つ構造物全体の

に拡張するのであるが、これはつまり
「材端力ベクトルの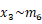と材端変位ベクトルの 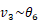を追加し、それに対応して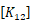の拡張を行う」ことである。

具体的には
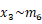は材端力ベクトルの7～18行目なので、これに対応する 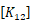の7～18行目を追加する。
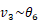は材端変位ベクトルの7～18行目なので、これに対応する 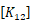の7～18列目を追加する。

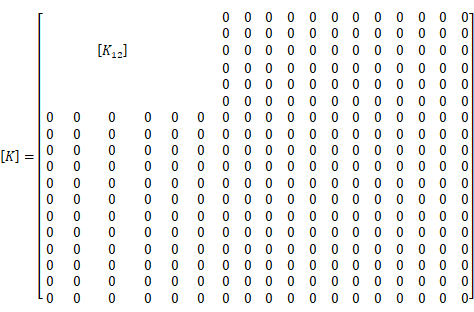
同様に、部材2-3の部材剛性マトリクス 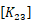に関しては
材端力ベクトルの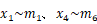 と材端変位ベクトルの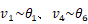を追加し、それに対応して 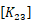の拡張を行う。

具体的には
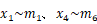は材端力ベクトルの1～3行目、10～18行目なので、これに対応する 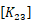の1～3行目、10～18行目を追加する。
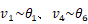は材端変位ベクトルの1～3行目、10～18行目なので、これに対応する 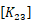の1～3列目、10～18列目を追加する。

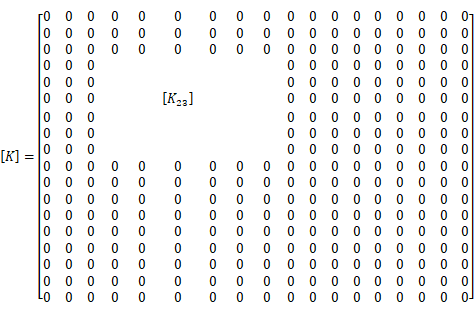
この様に、全ての部材剛性マトリクスを18次の正方行列に拡張した上でそれらを合算すれば、 構造物全体の剛性マトリクス(全体剛性マトリクス) が完成する。