鉄塔設計, 鉄塔基礎設計, 有限要素法解析, 構造物強度計算, 耐震設計 株式会社スタークス

8. 材端力(外力)ベクトルの作成

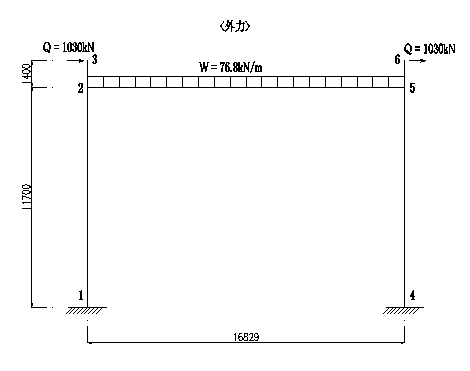
今回解析するモデルではQとWという荷重が構造物に作用する。
ここでQは節点荷重であり、Wは分布荷重である。

この荷重を剛性方程式に組み込んでみよう。

まずは節点荷重のQについて考える。
Qは節点番号3と6のx方向に作用する大きさ1030kNの荷重なので、以下の様に組み込む。

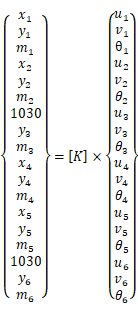
この様に、節点に作用する荷重(外力)は対応する変数と置き換えるだけである。

次に分布荷重Wについて考える。
有限要素法では節点荷重しか考慮することが出来ないので、分布荷重は節点荷重に変換する必要がある。

どうやって変換するのかというと、等分布荷重が作用している部材が固定端だとした場合の反力を計算し、それを節点荷重として剛性方程式に組み込む。

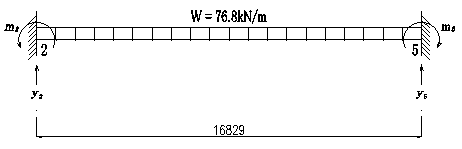
つまり、上図のモデルの固定端反力を計算しそれをy2、y5、m2、m5として剛性方程式に組み込む。
実際に計算してみると


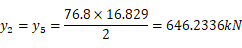
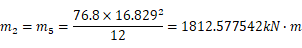になる。

力の方向を考慮して符号を付けると、剛性方程式は以下の様になる。


最終的には0の外力を組み込んで以下の様になる。

最後まで残った、x1,y1,m1とx4,y4,m4は支点位置の材端力ベクトルである。 これらは特に意味も無く通常は使われないのだが、後に説明する「剛性方程式の変形」を分かり易くするためにこのままにしておく。